Localization lemmas

Recall that the generalization of the first and second laws of thermodynamics for continua are integral equations. In other words, they are global statements of energy balance and entropy increase. What we wish to acquire is a local description of these laws. Towards this end, we will be now develop an important lemma that will prove to be very useful later on.

Basic localization lemma

Suppose that we are dealing with the motion of a material body $\mathcal{B}$ in three dimensional space, as viewed by an observer. Let $B_t$ be the current placement of the body. Suppose further that we are given the following integral equation $$\frac{d}{dt} \int_{B_t} a(\mathsf{x},t) \,dv = \int_{B_t} b(\mathsf{x},t) \, dv + \int_{\partial B_t} \mathsf{c}(\mathsf{x},t)\cdot\mathsf{n}(\mathsf{x},t)\,da,$$ where $a(\cdot,t):B_t \to \mathbb{R}$ and $b(\cdot,t):B_t \to \mathbb{R}$ are scalar fields, and $\mathsf{c}(\cdot,t):B_t \to TB_t$ is a vector field on $B_t$. Note that the vector field $\mathsf{c}(\cdot,t)$ is defined on the whole of $B_t$, even though the equation displaced above uses just the values of this vector field on the surface $\partial B_t$. We are interested in deriving the local version of this integral equation.

A crucial information we will need to carry out the localization process is that the integral equation is true for any sub-region of $B_t$. Thus, if $\Omega \subseteq B_t$ is an open subset of $B_t$, then we will take it as given that the following equation is true: $$\frac{d}{dt} \int_{\Omega} a(\mathsf{x},t) \,dv = \int_{\Omega} b(\mathsf{x},t) \, dv + \int_{\partial \Omega} \mathsf{c}(\mathsf{x},t)\cdot\mathsf{n}(\mathsf{x},t)\,da.$$ In practice, this assumption is not really a limitation since its validity stems from simple physical considerations, as we will see later. Notice how the requirement that $\mathsf{c}(\cdot,t)$ is a vector field on the whole of $B_t$ is necessary for the foregoing equation to be well-defined.

To achieve the desired localization, we make use of the divergence theorem that we studied earlier: for any open $\Omega \subseteq B_t$, $$\int_{\partial \Omega} \mathsf{c}(\mathsf{x},t)\cdot\mathsf{n}(\mathsf{x},t)\,da = \int_{\Omega} \text{div }\mathsf{c}(\mathsf{x},t)],dv.$$ Using this in conjunction with the integral equation presented earlier, we get $$\frac{d}{dt} \int_{\Omega} a(\mathsf{x},t) \,dv = \int_{\Omega} b(\mathsf{x},t) \, dv + \int_{\Omega} \text{div }\mathsf{c}(\mathsf{x},t)\,dv.$$ Taking the time derivative on the left hand side inside the integral, using techniques outlined earlier, we see that the following is true for any open subset $\Omega \subseteq B_t$: $$\int_{\Omega} \left(\frac{Da(\mathsf{x},t)}{Dt} + a(\mathsf{x},t)\text{div }\mathsf{v}(\mathsf{x},t) - b(\mathsf{x},t) - \text{div }\mathsf{c}(\mathsf{x},t)\right)dv = 0.$$ Since this is true for any sub-region $\Omega \subseteq B_t$, let us choose $\Omega$ to be an infinitesimally small volume centered at $\mathsf{x} \in B_t$. A simple application of the mean value theorem immediately yields the following local version of the integral equation $$\frac{Da(\mathsf{x},t)}{Dt} + a(\mathsf{x},t)\text{div }\mathsf{v}(\mathsf{x},t) = b(\mathsf{x},t) + \text{div }\mathsf{c}(\mathsf{x},t).$$ Note that this is a partial differential equation that is defined pointwise, unlike the global integral equation. The process of going from the integral equation to the corresponding differential equation is known as localization.

Cauchy's localization lemma

We will now prove a very important result that will turn out to be veru useful in deriving the various balance principles of continuum mechanics later on. Let us consider the following integral equation $$\int_{\Omega} a(\mathsf{x},t)\,dv = \int_{\partial \Omega} \tilde{c}(\mathsf{x},t,\mathsf{n}(\mathsf{x},t))\,da.$$ Here, $\Omega \subseteq B_t$ is an arbitrary open subset of the the current placement of the body $B_t$, $a(\cdot,t):B_t \to \mathbb{R}$ is a scalar field, and $\tilde{c}(\cdot, t, \cdot):TB_t \to \mathbb{R}$ is a scalar field on $TB_t$. This just means that given any $\mathsf{x} \in B_t$ and $\mathsf{v} \in T_{\mathsf{x}}B_t$, $\tilde{c}(\mathsf{x},t,\mathsf{v}) \in \mathbb{R}$. In the integral equation displayed above, the quantity $\mathsf{n}(\mathsf{x},t)$ stands for the unit normal to the surface $\partial \Omega$ at $\mathsf{x} \in \partial \Omega$, as before. We will now localize this equation. Notice that we cannot directly apply the localization procedure introduced in the previous section since the surface integral involving the $\tilde{c}$ field is not in the right form.

The Cauchy localization lemma states that under the conditions specified earlier, there exists a vector field $\mathsf{c}(\cdot,t):B_t \to TB_t$ such that $$\tilde{c}(\mathsf{x},t,\mathsf{n}) = \mathsf{c}(\mathsf{x},t)\cdot\mathsf{n},$$ for every $\mathsf{x} \in B_t$ and $\mathsf{n} \in T_{\mathsf{x}}B_t$.

Before we look into the proof of the Cauchy localization lemma, let us note that this lemma immediately provides us with a means to localize the integral equation that we started with, as the following calculation shows: $$\begin{split} \int_{\Omega} a(\mathsf{x},t) &= \int_{\partial \Omega} \tilde{c}(\mathsf{x},t,\mathsf{n}(\mathsf{x},t))\\ &= \int_{\partial \Omega} \mathsf{c}(\mathsf{x},t)\cdot\mathsf{n}(\mathsf{x},t)\,da\\ &= \int_{\Omega} \text{div }\mathsf{c}(\mathsf{x},t)\,dv. \end{split}$$ This calculation thus allows us to localize the original integral equation to obtain the following differential equation: $$a(\mathsf{x},t) = \text{div }\mathsf{c}(\mathsf{x},t).$$ We thus see how the Cauchy localization lemma helps us localize certain kinds of integral equations.

Let us now turn to a proof of the Cauchy localization lemma. The key idea that is exploited in the proof is the elementary fact that if a domain in $B_t$ is shrunk to point, its volume goes to zero faster than its surface area. Let us see how this works in a more rigorous setting. For the purposes of this argument, let us consider a small volume $T$ shaped like a tetrahdron, with one of its vertices at $\mathsf{x} \in B_t$, and three of its edges along the coordinate axes, as shown in the figure below.

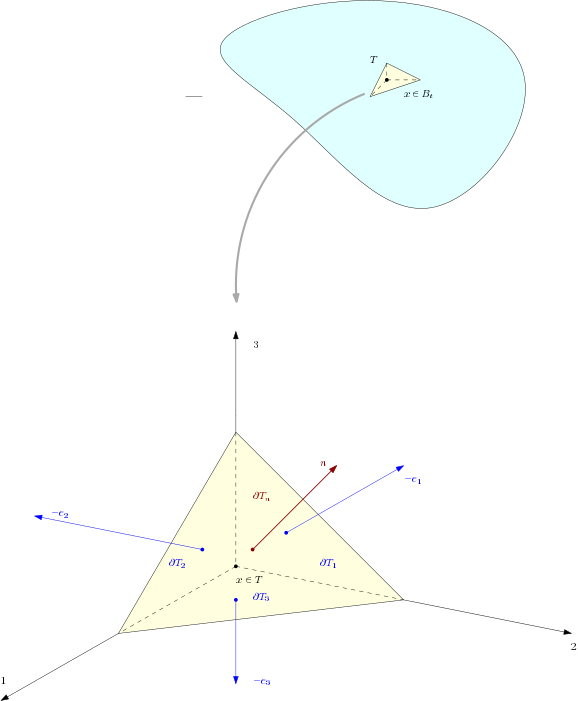
The region $T$ is sometimes called the Cauchy tetrahedron. Let $\mathsf{n}$ be the normal vector to the face of the tetrahedron that intersects the three coordinate axes, as shown in the figure. We will denote this surface as $\partial T_n$. The face of the tetrahedron $T$ whose normal is $-\mathsf{e}_i$ will be denoted by $\partial T_i$, where $i = 1,2,3$, as also depicted in the figure. With these definitions in place, we see that $$\partial T = \partial T_n \cup_{i=1}^3 \partial T_i.$$ Let the length of the edges of $T$ along the directions $\mathsf{e}_1,\mathsf{e}_2,\mathsf{e}_3$ be $l_1,l_2,l_3$. It is convenient to define $l = \text{max}(l_1,l_2,l_3)$. In the limit when $l\to 0$, the Cauchy tetrahedron $T$ shrinks to the point $\mathsf{x} \in B_t$.

Let us now consider the integral equation $$\int_T a(\mathsf{x},t)\,dv = \int_{\partial T} \tilde{c}(\mathsf{x},t,\mathsf{n}(\mathsf{x},t))\,da$$ in the limit $l \to 0$. The surface integral in this equation can be additively decomposed as follows: $$\begin{split} \int_{\partial T} \tilde{c}(\mathsf{x},t,\mathsf{n}(\mathsf{x},t))\,da &= \int_{\partial T_n \cup_{i=1}^3 \partial T_i} \tilde{c}(\mathsf{x},t,\mathsf{n}(\mathsf{x},t))\,da\\ &= \int_{\partial T_n} \tilde{c}(\mathsf{x},t,\mathsf{n})\,da + \sum_{i=1}^3 \int_{\partial T_i} \tilde{c}(\mathsf{x},t,-\mathsf{e}_i) \,da. \end{split}$$ Let us now evaluate the surface and volume integrals in the limit $l \to 0$. Using the mean value theorem, the surface integral can be approximated as $$\int_{\partial T} \tilde{c}(\mathsf{x},t,\mathsf{n}(\mathsf{x},t))\,da \simeq \tilde{c}(\mathsf{x}^{(n)},t,\mathsf{n})\,\text{area}(\partial T_n) + \sum_{i=1}^3 \tilde{c}(\mathsf{x}^{(i)},t,-\mathsf{e}_i) \, \text{area}(\partial T_i).$$ Here, $\text{area}(S)$ stands for the area of a surface $S$ embedded in $B_t$, $\mathsf{x}^{(n)} \in \partial T_n$, and $\mathsf{x}^{(i)} \in \partial T_i$, where $i = 1,2,3$.

The volume integral can also be approximated in the limit $l \to 0$ using the mean value theorem as $$\int_T a(\mathsf{x},t)\,dv \simeq a(\xi,t) \, \text{vol}(T).$$ Here, $\text{vol}(T)$ denotes the volume of the region $T$, and $\xi \in T$.

Putting all these together, we see that the integral equation reduces to the following in the limit $l \to 0$: $$a(\xi,t) \, \text{vol}(T) = \tilde{c}(\mathsf{x}^{(n)},t,\mathsf{n})\,\text{area}(\partial T_n) + \sum_{i=1}^3 \tilde{c}(\mathsf{x}^{(i)},t,-\mathsf{e}_i) \, \text{area}(\partial T_i).$$ If $\mathsf{n} = \sum n_i \mathsf{e}_i$, then note that the areas of $\partial T_i$ and $\partial T_n$ are related, by simple geometric considerations, as $$n_i = \frac{\text{area}(\partial T_i)}{\text{area}(\partial T_n)}.$$ We therefore see that $$a(\xi,t) \frac{\text{vol}(T)}{\text{area}(\partial T_n)} = \tilde{c}(\mathsf{x}^{(n)},t,\mathsf{n}) + \sum_{i=1}^3 \tilde{c}(\mathsf{x}^{(i)},t,-\mathsf{e}_i)n_i.$$ In the limit $l \to 0$, $$\lim_{l \to 0} \frac{\text{vol}(T)}{\text{area}(\partial T_n)} = 0,$$ since volumes go to zero faster than surface areas. To appreciate why this is the case, note that $\text{vol}(T) \propto l^3$, whereas $\text{area}(\partial T_a) \propto l^2$, where $a = 1,2,3,n$. Further more, the following limits hold: $$\lim_{l \to 0} \xi = \lim_{l \to 0} \mathsf{x}^{(n)} = \lim_{l \to 0} \mathsf{x}^{(1)} = \lim_{l \to 0} \mathsf{x}^{(2)} = \lim_{l \to 0} \mathsf{x}^{(3)} = \mathsf{x}.$$ We thus finally obtain the following equation in the limit $l \to 0$: $$0 = \tilde{c}(\mathsf{x},t,\mathsf{n}) + \sum_{i=1}^3 \tilde{c}(\mathsf{x},t,-\mathsf{e}_i)n_i.$$ In the special case when $\mathsf{n} = \mathsf{e}_i$, we immediately obtain the following result: $$\tilde{c}(\mathsf{x},t,\mathsf{e}_i) = -\tilde{c}(\mathsf{x},t,-\mathsf{e}_i).$$ We thus finally obtain the following expression for $\tilde{c}(\mathsf{x},t,\mathsf{n})$: $$\begin{split} \tilde{c}(\mathsf{x},t,\mathsf{n}) &= -\sum_{i=1}^3 \tilde{c}(\mathsf{x},t,-\mathsf{e}_i)n_i\\ &= \sum_{i=1}^3 \tilde{c}(\mathsf{x},t,\mathsf{e}_i)n_i. \end{split}$$ Let us now define a vector field $\mathsf{c}(\cdot,t):B_t \to TB_t$ as follows: for any $\mathsf{x} \in B_t$, $$\mathsf{c}(\mathsf{x},t) = \sum_{i=1}^3 \tilde{c}(\mathsf{x},t,\mathsf{e}_i)\mathsf{e}_i.$$ It follows immediately that $$\tilde{c}(\mathsf{x},t,\mathsf{n}) = \mathsf{c}(\mathsf{x},t)\cdot \mathsf{n},$$ thereby proving Cauchy's localization lemma.

Remark

The Cauchy localization lemma can also be extended to tensor fields in an entirely analogous manner. We will make use of this localization principle shortly to deduce the existence of both the Cauchy stress tensor and the heat flux vector.